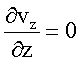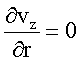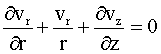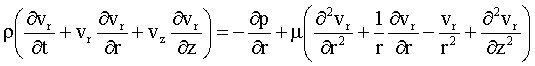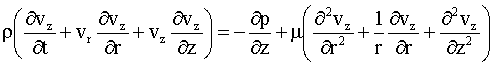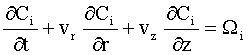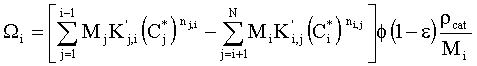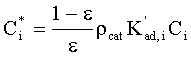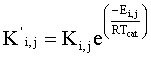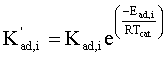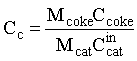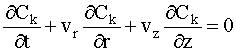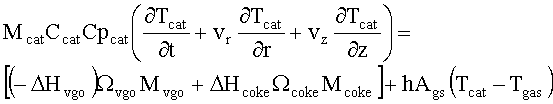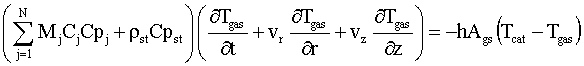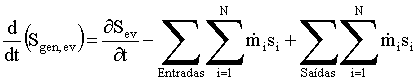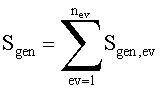I. MODELO PROPOSTO

    A literatura técnica (e.g., Gao et al., 1999; Gao et al., 1999; Mathiesen et al., 1999; Ali and Rohani, 1997; Blasetti and Lasa, 1997; Cerqueira, et al., 1997; Martignoni and Lasa, 2001) disponibiliza uma grande variedade de modelos dinâmicos e cinéticos para a simulação do craqueamento catalítico de petróleo no interior do riser. Como o objetivo deste trabalho é a criação de uma ferramenta que possa ser utilizada tanto para projeto como para controle e otimização, foi proposto um modelo capaz de gerar um código computacional rápido, porém preciso o suficiente para captar de forma adequada os fenômenos físicos e químicos que ocorrem no interior do riser.

    Os modelos mais simples consideram um escoamento do tipo plug-flow, com uma cinética das reações químicas com poucos lumps. Neste modelo, o riser é discretizado com um sistema de coordenadas cilíndricas bidimensional com uma entrada no fundo (na extremidade inferior) e uma entrada lateral. Para as reações de craqueamento catalítico foi utilizado um modelo com 6 lumps (SIX/PETROBRAS). Mesmo os modelos mais complexos disponíveis na literatura raramente contemplam a possibilidade de entradas laterais no riser. A entrada lateral é uma configuração bastante comum em risers existentes em refinarias em todo o mundo. Assim, o presente modelo pretende permitir a análise e otimização do posicionamento e inclinação das entradas laterais visando investigar a possibilidade de melhoria ou até de maximização da produção de combustíveis selecionados tanto para o projeto de novos risers como para instalações existentes.

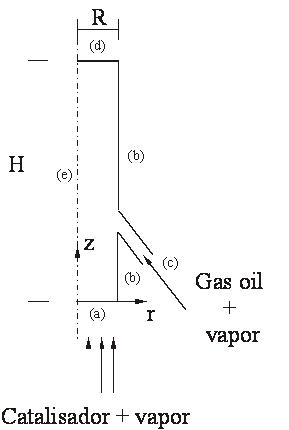
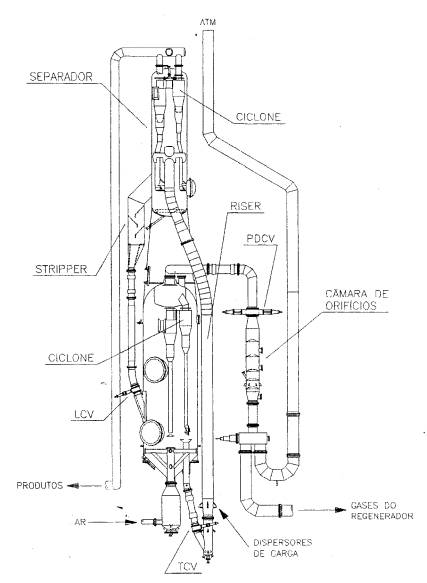
    A Figura I.1 (a) mostra um esquema simplificado da geometria e das condições de contorno do modelo proposto para o riser. A Figura I.1 (b) mostra o posicionamento do equipamento em análise dentro do conjunto de equipamentos de uma Unidade de Craqueamento Catalítico típica.

	(a)
	(b)
	(c)
	(d)
	(e)
(a) (b)
Figura I.1: Geometria e condições de contorno para o riser (a) e diagrama esquemático de uma Unidade de Craqueamento Catalítico típica (b).

    No presente modelo o escoamento é considerado monofásico, ou seja, o campo de velocidades é único tanto para o catalisador como para o gasóleo, e as propriedades físicas como viscosidade e massa específica, entre outras, são consideradas como sendo propriedades médias para a mistura fluidizada catalisador/gasóleo. A fase sólida está presente no modelo, assim como cada um dos lumps, como uma espécie, a qual é definida através de uma equação de transporte.

I.1 Modelo fluidodinâmico

    Todos os modelos para a fluidodinâmica no riser, por mais complexos e completos que sejam, sempre apresentam hipóteses simplificadoras. Com base no entendimento do fenômeno físico e análises de ordem de grandeza, normalmente é possível determinar quais são os fenômenos mais importantes, e com este conhecimento, desprezar da formulação matemática os termos menos significativos. É importante porém, sempre ter bem claro quais as simplificações que foram feitas e quais os efeitos que essas hipóteses simplificadoras podem causar na solução do modelo proposto. A Tabela I.1 faz uma comparação entre os diversos modelos encontrados na literatura.

Tabela I.1: Comparação entre diversos modelos com relação a fluidodinâmica
Plug-flow	Modelo proposto	Fases contínuas	Teoria cinética
unidimensional	bidimensional	bi ou tridimensional	bi ou tridimensional
1 ou 2 fases	1 fase	2 ou 3 fases	2 fases*
1 entrada única para o gasóleo e para o catalisador	entradas distintas para o gasóleo e o catalisador	entradas distintas ou única para o gasóleo e o catalisador	1 entrada única para o gasóleo e para o catalisador*
escoamento não viscoso	escoamento viscoso	escoamento viscoso	escoamento viscoso
sem modelo de turbulência	sem modelo de turbulência	com ou sem modelo de turbulência	com ou sem modelo de turbulência para o gás

* refere-se aos trabalhos encontrados nesta revisão, não implica que a metodologia não possa ser aplicada diferentemente

No presente modelo as seguintes hipóteses simplificadoras foram adotadas:

- escoamento incompressível;

- bidimensional, em coordenadas cilíndricas (r e z);

- velocidade relativa entre partícula e gás nula (monofásico);

- o catalisador (fase sólida) é descrito como um meio contínuo e uma equação de transporte, semelhante a dos lumps, é escrita para ele;

- o gasóleo entra no riser já totalmente fluidizado e na fase gasosa (vapor);

    Com base nestas hipóteses o sistema de equações para o modelo fluidodinâmico proposto é representado pelas seguintes equações:

- equação da continuidade global

(I.1)

- equação da concervação da quantidade de movimento nas direções r e z

(I.2)

(I.3)

onde, r e z representam o sistema de coordenadas cilíndricas (m); p a pressão (Pa); r a massa específica (kg/m³); v_r e v_z as velocidades nas direções r e z respectivamente (m/s); t o tempo (s) e m a viscosidade absoluta (N s/m²).

I.2. Modelo cinético

    Dentre os muitos modelos possíveis para a cinética de reação de craqueamento catalítico encontrados na literatura, podemos destacar dois tipos: 1) simplificados com 4 ou 5 lumps e 2) detalhados, normalmente com mais de 10 lumps. Os modelos simplificados têm a vantagem de ser simples e com poucas constantes cinéticas a serem determinadas, porém normalmente apresentam uma grande dependência da carga, ou seja, para cada tipo específico de gasóleo, todos os parâmetros cinéticos necessitam ser novamente determinados. Nos modelos mais detalhados, somente o gasóleo é compostos de 4 ou 5 lumps, permitindo assim uma aplicação mais geral para os parâmetros cinéticos determinados, tornando o modelo menos dependente do tipo de carga.

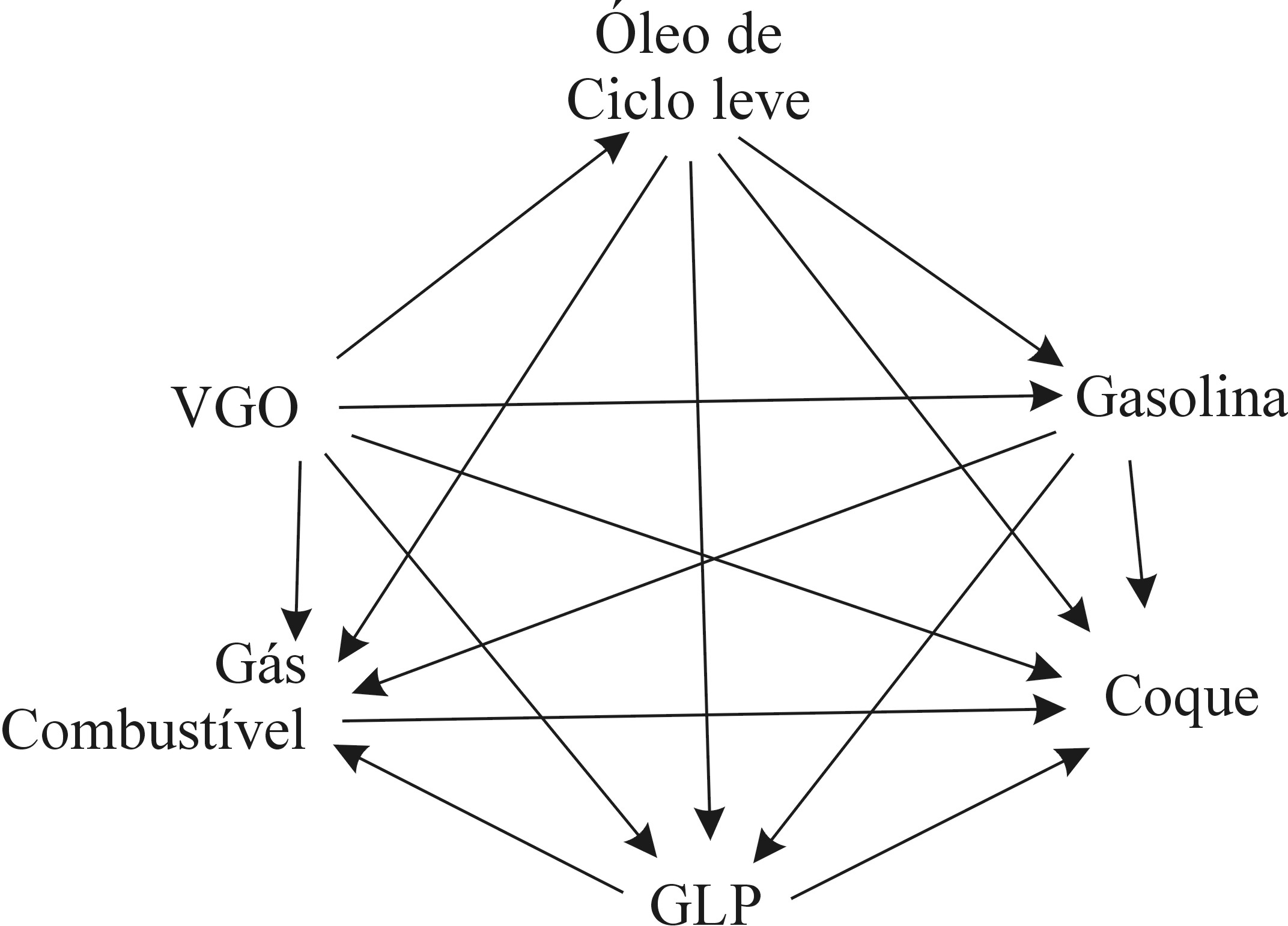
   O modelo cinético para a modelagem das reações de craqueamento catalítico do gasóleo utilizado neste projeto, é um modelo de 6 lumps proposto pela equipe de pesquisa científica da SIX/Petrobras (2001).

Figura I.2: Modelo cinético

    Embora o presente modelo cinético seja construído com apenas 6 lumps, seus lumps foram escolhidos de tal forma que os produtos de maior interesse podem ser determinados separadamente.

    O conjunto de equações para o esquema mostrado na Fig. I.1 é dado por:

	(I.4)
	(I.5)
	(I.6)
	(I.7)
	(I.8)
	(I.9)
	(I.10)

onde, C_i é a concentração do lump i (kmol/m³); W o termo de reação do lump i (kmol/m³ s); C_c a concentração de coque no catalisador (kg_coque/kg_cat); E a energia de ativação (kJ/kmol K); K a constante pré-exponencial de reação (m³/kg_cat s ou m⁶/kmol kg_cat s); M a massa molecular (kg/kmol); n  a ordem da reação; N o número de lumps; R a constante universal dos gases (kJ/kmol K); T a temperatura (K); e a porosidade e f a função de desativação do catalisador. Os índices inferiores "ad" e "cat" indicam adsorção e catalisador, respectivamente e o índice superior "in" indica entrada.

    Para o catalisador e vapor d'água, uma equação de conservação semelhante a Eq. (I.9) deve ser escrita. Como o catalisador é apenas um agente que aumenta a taxa de reação, não reagindo com os demais componentes da mistura, e o vapor d'água é um auxiliar na atomização do gasóleo, nas equações de conservação de espécies para estes dois componentes não existe o termo de reação (W).

(I.11)

onde k = cat ou st para representar o catalisador e o vapor d´água, respectivamente.

I.3. Equações da energia

    Finalmente, para completar o modelo matemático são necessárias duas equações de conservação de energia; uma para o sólido (catalisador) e outra para o gás (gasóleo + vapor). Embora tenha sido adotado um modelo monofásico para a formulação do escoamento, optou-se por utilizar duas equações de conservação de energia para caracterizar a interação energética entre as duas fases presentes (gás e particulado). Na Eq. I.5 a temperatura do catalisador é utilizada para o cálculo das reações de craqueamento, enquanto que para modelar as trocas térmicas entre as fases gasosas e sólida uma segunda equação para o gás é necessária. Estas duas equações são escritas como:

	(I.12)
	(I.13)

onde, as variáveis que não foram ainda definidas são: Cp o calor específico a pressão constante (kJ/kg K); DH a entalpia de reação (kJ/kg), conforme dados experimentais (SIX/PETROBRÁS, 2001); h o coeficiente de troca de calor entre as fases sólida e gasosa (kJ/m² s K); A_gs a área específica do particulado (m²/m³). Os índices inferiores "cat", "gas", "st", "coke" e "vgo" indicam fase sólida (catalisador), fase gasosa, vapor, coque e gasóleo, respectivamente.

I.4. Cálculo da geração de entropia

    Na indústria do petróleo, é reconhecida a importância do riser numa planta de craqueamento catalítico de gasóleo. Em virtude disto, muitos trabalhos de dimensionamento e simulação de condições ótimas de operação podem ser encontrados na literatura. No entanto, estes trabalhos normalmente abordam dois pontos críticos na simulação do riser: a fluidodinâmica e a cinética de reação do craqueamento catalítico.

    Uma possibilidade, que não foi até o momento explorada na literatura técnica, é a análise de geração de entropia no riser. Espera-se que uma análise a partir da segunda lei da Termodinâmica possa permitir a otimização (maximização da produção de produtos nobres como gasolina e óleo diesel) do riser sob um ponto de vista alternativo. Pretende-se neste trabalho dar os primeiros passos neste sentido. A seguir, é apresentada uma proposta para o cálculo da geração de entropia total no processo de craqueamento catalítico que ocorre no interior do riser, i.e., devido ao escoamento viscoso do gasóleo, aos gradientes de temperaturas e às reações químicas do craqueamento do gasóleo.

    É importante deixar claro, que o estudo da geração de entropia no riser é efetuado após todos os demais cálculos terem sido feitos. Após a determinação dos campos de temperatura e velocidades, esses valores são utilizados em pós-processamento para a determinação da entropia gerada, e assim quantificando as perdas termodinâmicas ocorridas no processo.

    Para a determinação da geração de entropia devido ao processo de craqueamento catalítico é necessário a determinação de fluxos mássicos (ou molares) de espécies que podem surgir ou desaparecer durante o tempo de passagem pelo riser. Esses fluxos são determinados como descrito anteriormente no modelo.

A taxa de geração de entropia total em cada elemento de volume do domínio em análise (interior do riser), definido pela malha escolhida para discretizar o domínio de solução é calculada como se segue (Bejan, 1996)

(I.14)

onde s_i é a propriedade entropia do componente i (kJ/kg K), é o fluxo mássico do componente i (kg/s), e N o número de lumps. Para a simulação em regime permanente, o termo é nulo. Além disso, para a simulação em regime transiente, adota-se a hipótese simplificadora de desprezar o termo em presença dos outros termos no segundo membro da Eq. (I.14).

    Finalmente, a geração de entropia total no interior do riser é dada por:

(I.15)

onde n_ev é o número total de elementos de volume definido pela malha escolhida para discretizar o domínio de solução, i.e., o interior do riser.