(OTIMIZAÇÃO E CONTROLE DE UNIDADES DE CRAQUEAMENTO CATALÍTICO)

2. METODOLOGIAS:

2.1. Modelagem e Controle da Unidade de Craqueamento Catalítico:

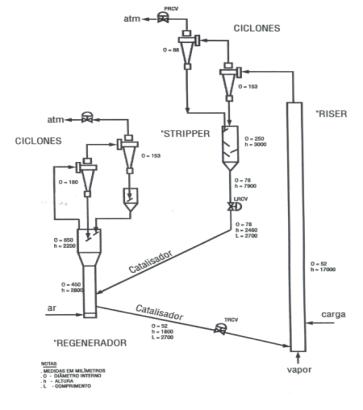
Figura 1 – Diagrama simplificado do circuito regenerador – “riser” – “stripper”, da unidade multipropósito de FCC – U-144 da SIX/PETROBRÁS.

A Figura 1 mostra um diagrama esquemático da unidade multipropósito de FCC completa, existente na SIX/PETROBRÁS, em São Mateus do Sul-PR, que será utilizada para obtenção de dados reais para a simulação numérica e também, para validação experimental dos resultados desta simulação numérica. Neste projeto, dentre os equipamentos da Fig. 1, será dedicado um maior grau de importância para o tubo de elevação (“riser”), que é o elemento principal da unidade, i.e., onde ocorrem as reações de craqueamento dos hidrocarbonetos pesados (gasóleo), para a formação dos hidrocarbonetos leves. Numa planta rentável atualmente, apenas 45 % da carga de entrada se transforma em gasolina. Há, portanto, uma grande margem a melhorar neste processo, i.e., para maximizar a produção de gasolina e GLP (gás liquefeito de petróleo).

O problema consiste em obter as concentrações de reagentes e produtos, os perfis de velocidade e a distribuição de temperatura ao longo do tubo de elevação (“riser”). Estas distribuições são determinadas pelas condições ambientais externas, a geometria do sistema, vazões de entrada de catalizador e gasóleo (carga), além de vários outros parâmetros de projeto e de operação.

A metodologia a ser adotada para atingir os objetivos propostos neste projeto, consiste em desenvolver as seguintes etapas:

· Desenvolvimento de um modelo físico simplificado para o tubo de elevação (“riser”) e outros equipamentos;

· Implementação computacional do modelo matemático construído a partir do modelo físico simplificado;

· Validação dos resultados numéricos e ajuste do modelo matemático, e

· Otimização termodinâmica do processo.

Modelo físico simplificado

O desenvolvimento da nova metodologia se iniciará com a elaboração de um modelo físico simplificado para o sistema, que combine conceitos teóricos da Termodinâmica Clássica e correlações empíricas de Mecânica dos Fluidos,Transferência de Calor e Massa, Química, que são válidas desde o regime laminar ao turbulento do escoamento. O modelo físico simplificado permitirá escrever o modelo matemático do processo, como um sistema de equações diferenciais ordinárias, tendo o tempo como variável independente, e a temperatura e concentrações de reagentes e produtos como variáveis dependentes. Por simplicidade, a princípio, será adotado um modelo com 6 componentes (“lumps”), entre reagentes e produtos, i.e., gasóleo pesado, GLP, gás combustível, gasolina, óleo diesel e coque. No entanto, as características do sistema reacional levam inevitavelmente a um sistema de múltiplos parâmetros, os quais representam grupos de compostos e, portanto, acabam por embutir fenômenos não levados em consideração dentro dos mesmos, isto sem mencionar os parâmetros extras de adsorção.

Nesta etapa, também será construido em laboratório, um tubo de elevação (“riser”) em escala reduzida para simulação e visualização do escoamento de gases em conjunto com o catalizador (sólido). O equipamento será devidamente instrumentado para aquisição de dados que auxiliarão na modelagem do escoamento, para determinação das velocidades intersticiais entre o sólido e os gases e para determinação da porosidade ao longo do tubo, i.e., a frações de catalizador (sólido) e gases no interior do tubo, em função da posição.

Implementação computacional

O domínio em análise será discretizado com um esquema tri-dimensional simples de volumes finitos de células centradas, para a obtenção da solução numérica. Haverá, portanto, um sistema de equações diferenciais ordinárias, obtido a partir do modelo matemático, para cada volume obtido com a discretização. Após a discretização do domínio estará montado um grande sistema de equações diferenciais ordinárias a ser integrado no tempo a partir de condições iniciais obtidas a partir de dados da instalação existente na SIX/PETROBRÁS.

A inovação no presente modelo é que os tamanhos dos volumes de controle não precisam ser extremamente reduzidos para obter resultados suficientemente precisos, como seria necessário com a utilização de outros métodos numéricos (e.g., volumes finitos, elementos finitos) que discretizam modelos matemáticos constituídos de equações diferenciais parciais. A grande vantagem é que com um número razoavelmente pequeno de elementos, espera-se obter convergência associada a um tempo computacional reduzido.

A combinação do modelo físico simplificado com o esquema de volumes finitos adotado na discretização do domínio é, portanto, denominada como modelo de elementos de volume (MEV). As equações governantes resultam dos princípios de conservação de massa, momentum, energia e concentração de espécies, aplicados a cada elemento de volume. Cada elemento de volume leva em consideração as reações químicas, geração ou consumo de energia, e os processos de transferência de calor e massa, através das 6 faces de um elemento cúbico, por condução, convecção e radiação. A seguir, ainda nesta fase, será realizada uma simulação numérica do tubo de elevação para algumas condições de operação da instalação existente.

Validação dos resultados numéricos e ajuste do modelo matemático

Nesta etapa, será realizada a validação dos resultados numéricos do modelo matemático, obtidos com a simulação da unidade piloto existente na SIX, ao mesmo tempo melhorando o equacionamento matemático, para que melhor capture os fenômenos físicos envolvidos no processo. Será um processo iterativo, convergindo quando os resultados numéricos se aproximarem dos experimentais. Esta é uma etapa indispensável do estudo, antes da realização da otimização do sistema, pois permitirá avaliar a precisão dos resultados numéricos obtidos com o modelo desenvolvido.

Otimização termodinâmica

Para a realização da otimização termodinâmica do processo, será utilizado o modelo desenvolvido e validado nas etapas anteriores. Ao modelo, nesta etapa, será acrescentada uma análise exergética, que permitirá computar a geração de entropia em cada elemento de volume (ou exergia destruída), para identificar as perdas termodinâmicas que ocorrem no processo, visando minimizá-las. A seguir, será necessária a identificação das restrições existentes para o sistema (e.g., alocação finita de espaço útil, tamanhos finitos, formas pré-definidas, velocidades finitas, materiais especificados), formulando-as matematicamente e acrescentando ao modelo.

A idéia nova é que a geração de entropia leva em consideração todos os efeitos que demandam o uso de energia. Efeitos diferenciados, tais como aumento de massa de catalizador e aumento de arrasto, por exemplo, são levados em consideração na mesma base, rigorosa e termodinâmicamente correta. A arquitetura completa de um sistema (e.g., o sistema em análise neste projeto) será DEDUZIDA da minimização da taxa total de geração de entropia.

2.2.Bico Dispersor

Para aumentar a velocidade do meio dispersador, no caso, o vapor superaquecido d'água, e aproveitar o máximo possível a entalpia do mesmo, será pesquisada a viabilidade de emprego de escoamentos supersônicos. Aproveitando a teoria de escoamento supersônico será apresentada a metodologia de dimensionamento e otimização de forma de bocais supersônicos. Serão estudadas a propagação do jato supersônico, a formação de ondas de choque e a interação do fluxo supersônico com jatos coaxiais e transversais de óleo.

Especificamente, serão estudados bocais supersônicos com um corpo central, com a injeção transversal do óleo pesado pulverizado em um injetor centrífugo. Esse esquema aumenta a turbulência de escoamento contribuindo sobre a qualidade de dispersão. Aproveitando instalações de SIX/PETROBRAS serão feitos um modelamento matemático e um estudo experimental da interação de escoamentos supersônicos em câmaras de teste.

2.3 Formação de coque e Gasóleo Pesado

O presente estudo tem como objetivo mapear as condições de formação de coque para se otimizar o projeto do tubo pré-aquecedor e o controle do regime de funcionamento, tendo em vista contribuir para o aumento do tempo de campanha e aumento da tiragem de gasolina e GLP.

A primeira fase deste mapeamento será o levantamento dos mecanismos químicos de formação de coque (condições de equilíbrio químico e termodinâmico): i) Nucleação; ii) Cinética; iii) Condições de Temperatura e Pressão; iv) Taxa de formação de coque. Levantar as condições hidro-dinâmicas e de transferência de calor que evitam as condições de formação de coque (estabilidade hidrodinâmica): i) Regime de escoamento (laminar, transiente, turbulento); ii) Taxa de transferência de calor; iii) Geometria do tubo pré-aquecedor (comprimento, diâmetro, forma transversal e longitudinal); iv) Propriedades físico-químicas da superfície interna do tubo pré-aquecedor; v) Influência de equipamentos auxiliares (e.g., bombas). Deseja-se incluir nos modelos matemáticos baseados na conservação das espécies químicas e conservação de energia os efeitos dos fatores acima mencionados. Desta forma, será possível desenvolver um modelo fenomenológico capaz de capturar a tendência de formação de coque e taxa de deposição na parede interna do tubo pré-aquecedor.

A modelagem partirá de estudos que consideram as equações de conservação de espécies, cinética das reações químicas e escoamento em regime quase-estacionário. As propriedades do gasóleo pesado do petróleo de Marlim e Cabiúnas serão conforme apresentadas posteriormente. O modelo fenomenológico incorporará os dados de determinação estatística da formação de coque, cuja formação em determinada quantidade é inevitável. Com tudo isso, o modelo matemático incluindo os efeitos de todos os mecanismos que participam da formação de coque permitirá reduzir ao mínimo a taxa de formação de coque (pelo controle de temperatura, pressão, vazão, etc.) ou efeito de incrustação (seleção de materiais com superfícies seletivas). Observações práticas levam a crer que fatores como velocidade do escoamento, taxa de aquecimento e propriedades da superfície podem ser fatores preponderantes, porém a completa modelagem irá apontar a relevância destes parâmetros bem como outros para otimizar o projeto do tubo pré-aquecedor.

2.4 Controle Avançado

Uma das tarefas mais importantes para operação eficiente de uma planta complexa é a definição de mudanças nos pontos de operação das unidades (otimização) e a implementação destas mudanças de forma eficiente (controle). O estado estacionário do processo definido pelos requisitos operacionais e/ou de planejamento pode estar consideravelmente afastado do estado atual, e o objetivo então é o de levar o processo de uma forma segura do estado atual para o novo estado de operação. Esta transição de estados é implementada através de mudanças nos “setpoints” dos controladores junto ao processo, e pressupõe um período de operação transiente do processo. Na indústria do petróleo é geralmente mais importante manter o comportamento transiente dentro de limites razoáveis do que conseguir uma resposta no tempo mínimo com violentas excursões na resposta do processo. Esta operação está associada ao fato que, mesmo durante o transiente, as restrições à operação continuam válidas, sendo que durante as diferentes fases do transiente, diferentes restrições que eram inativas, podem tornar-se ativas, sem esquecer que as próprias restrições são normalmente, função do estado do processo.

Este problema de transição de estado pode ser interpretado como um problema de controle em que se deseja atingir um estado final conhecido a priori (novo ponto de operação) através de transições que satisfazem as restrições sobre as variáveis de estado e controle. Dentro deste contexto, pretende-se neste projeto, aplicar as técnicas de controle preditivo na implementação das mudanças de ponto de operação.

As técnicas de controle preditivo são adequadas a este problema basicamente por dois motivos:

· Os controladores preditivos são baseados na minimização de uma função custo num horizonte de tempo. Esta função custo pode ser escolhida de modo a incorporar o conhecimento prévio do estado final desejado (novos “setpoints”).

· Na obtenção do esquema de controle é possível considerar restrições sobre as variáveis. Este ponto é especialmente importante porque o rendimento máximo de uma unidade é conseguido freqüentemente levando algumas das variáveis aos seus valores limites sobre as restrições. A transição ótima é também freqüentemente uma transição que mantém a unidade operando sobre as restrições, sendo que algumas das restrições ativas no ponto de operação inicial podem passar a ser passivas durante a transição, e outras restrições, que não tinham relevância no ponto de operação inicial, passam a ser ativas durante a transição.

Assim, um dos objetivos do projeto é que o controlador preditivo gere a evolução ótima no tempo dos “setpoints”, desde os valores iniciais até os valores finais de forma que a implementação junto ao processo imposta pelos controladores locais leve à transição da unidade, e isto ocorra satisfazendo as restrições de operação e otimizando um critério de desempenho. Outro objetivo é analisar técnicas de controle avançado para manter o sistema operando num determinado “setpoint” quando ocorrem perturbações não-previstas.

Por outro lado, para a determinação dos “setpoints” ótimos, e também para a regulação e rastreamento do sistema em malha fechada, é necessário ter-se modelos matemáticos do processo incluindo a descrição de todas as suas restrições operacionais, com um grau de precisão adequado. O modelo do processo relaciona as variações das variáveis independentes (entradas manipuladas e perturbações) com as das variáveis dependentes (controladas). Uma das questões básicas relacionadas com o modelo a usar para cálculo dos “setpoints” é a da precisão exigida para o modelo. Um modelo rigoroso permite, obviamente, uma melhor representação da planta do que um modelo simples, por outro lado um modelo rigoroso freqüentemente, exige tempos computacionais longos, o que pode inviabilizar sua aplicação em tempo real. Por sua vez o uso de um modelo muito simples pode levar à determinação de condições não-ótimas ou até mesmo fisicamente não-realizáveis.

Desta forma os modelos usados na indústria do petróleo devem por um lado permitir uma aplicação numa faixa ampla de condições operacionais, integrando todas as restrições operacionais, e por outro lado serem capaz de relacionar as principais dinâmicas de entrada e saída do processo, a fim de simplificar a implementação dos controladores no processo.

Para a obtenção de modelos mais aproximados do processo real para fins de controle robusto, pretende-se utilizar neste projeto os métodos de estimação em horizontes estendido (long range preditive identification) que são métodos específicos para o controle preditivo. Estes modelos de controle serão obtidos a partir do simulador construído com o MEV descrito anteriormente, e tem como resultado preditores que podem ser usados diretamente pelo controlador preditivo.

Controle Preditivo

Para a obtenção do controlador preditivo inicialmente realiza-se um conjunto de previsões da saída do processo num horizonte de tempo denominado Horizonte de Previsão utilizando o modelo do processo a ser controlado. Baseado nestas previsões, a lei de controle é obtida minimizando-se um critério de custo que quantifica o desempenho futuro do sistema em malha fechada. Com esta lei de controle também pode-se considerar restrições na amplitude e na variação dos sinais de atuação e saída do processo.

O critério de custo minimizado é de maneira geral, do tipo quadrático e relaciona os erros entre a saída prevista e o sinal de referência conjuntamente com o esforço de controle. O modelo do processo é normalmente obtido utilizando-se um método de identificação. Portanto, o desempenho do sistema em malha fechada depende do tipo de modelo utilizado, da formulação do preditor de saída e do critério de otimização utilizado.

Normalmente, utiliza-se um modelo linear para a representação do processo a ser controlado. Contudo, o processo real pode ser variante no tempo, ter não linearidades, apresentar dinâmicas não-modeladas, etc. Estes fatores acarretam incertezas nos parâmetros do modelo. Nestes casos, a incerteza nos parâmetros do modelo determina que estes sejam caracterizados por uma região de pertinência e não por um único valor, e tem-se uma família de modelos representando o processo real. Os métodos de estimação robusta permitem identificar esta família.

Os algoritmos de controle preditivo que incorporam explicitamente na lei de controle o conhecimento sobre as incertezas paramétricas do modelo são denominados Controle Preditivo Robusto. As leis de controle para este preditores com incertezas paramétricas no modelo são obtidas resolvendo um problema de otimização do tipo min-max, onde a função custo a ser otimizada pode utilizar uma norma euclideana ou a norma infinita.

Pretende-se neste projeto utilizar algoritmos de otimização do tipo Sequential Quadratic Programming para calcular as leis de controle no caso da norma euclideana, e técnicas de Programação linear no caso da norma infinita. A estabilidade do sistema em malha fechada será analisada seguindo a abordagem apresentada em que é baseada na análise do comportamento dos sinais de entrada e saída do sistema. Também deverão ser analisadas estratégias para a diminuição do esforço computacional do algoritmo de controle robusto.

2.5 Revestimentos para Altas Temperaturas

A Engenharia do Petróleo há muito recorre à Engenharia de Superfícies para aumentar a vida útil dos equipamentos de processo; a metodologia adotada para o estudo deste problema segue os itens a seguir:

· Revestimento de componentes: Substratos correspondentes aos de componentes da unidade FCC serão revestidos recorrendo à técnica de soldagem a plasma por arco transferido (PTA) e aspersão térmica por arco elétrico, com materiais previamente selecionados, e com materiais alternativos.

· Caracterização das superfícies: determinação da influência dos parâmetros de processamento na rugosidade superficial, presença de porosidades e trincas, aderência etc., recorrendo a técnicas de liquido penetrante e ultra-som e ensaios mecânicos, eletroquímicos, MEV

· Caracterização da microestrutura: caracterização da microestrutura dos revestimentos depositados pelos diferentes processos antes e após desempenho em meio erosivo a alta temperatura, recorrendo a técnicas de microscopia ótica e eletrônica de varredura.

· Caracterização mecânica: Determinação da dureza dos revestimentos produzidos, recorrendo a técnicas de micro e macrodureza, tensões residuais na superfície e abaixo dela, pela técnica do furo cego, e dutilidade dos revestimentos, através de ensaios de flexão.

· Análise de descontinuidades: A técnica eletroquímica a ser utilizada para a análise de descontinuidades dos revestimentos consiste, basicamente, de uma dissolução anódica voltamétrica (DAV) do sistema substrato/revestimento com a medida da densidade de carga envolvida no processo de passivação do substrato.

· Comportamento erosivo: Construção de equipamento de erosão por partículas a quente e realização de ensaios de erosão.

· Ensaios em campo: elaboração de corpos de prova em condições pré-determinadas para ensaiar em campo, a fim de correlacionar com resultados obtidos em laboratório.